Classification

6. Classification#

In regression, we typically aim to predict a continuous outcome (like a numerical value). However, we can extend the same concepts of regression to classification tasks, where the goal is to predict a discrete class label. By using specific target values (like \(y = \pm 1\)), we can transform regression into a method for classifying data.

In this chapter, we’ll explore how regression-based techniques can be adapted to solve classification problems.

6.1. The Concept of Classification with Regression#

In classification, the target variable \(y_i\) represents the class label. For binary classification, we often use the labels \(y_i = +1\) and \(y_i = 0\) (or \(y_i = -1\)) to represent the two different classes. The goal is to assign the correct class to new data points based on features \(\mathbf{x}_i\).

We can approach this problem similarly to regression by fitting a function \(f(\mathbf{x})\), but instead of predicting a continuous variable, we focus on predicting whether \(f(\mathbf{x})\) is positive or negative:

  • If \(f(\mathbf{x}) > 0\), predict class \(+1\).

  • If \(f(\mathbf{x}) < 0\), predict class \(0\).

This can be achieved by minimizing a loss function, which represents the error between the predicted values and the true class labels.

6.2. Classification Loss Functions#

When applying regression techniques to classification, the choice of loss function is critical. In regression, we typically minimize the sum of squared residuals, but in classification, we use loss functions that are designed to penalize misclassifications propotional to how much the predictor insists on the incorrect prediction. Below are three common loss functions used in classification tasks:

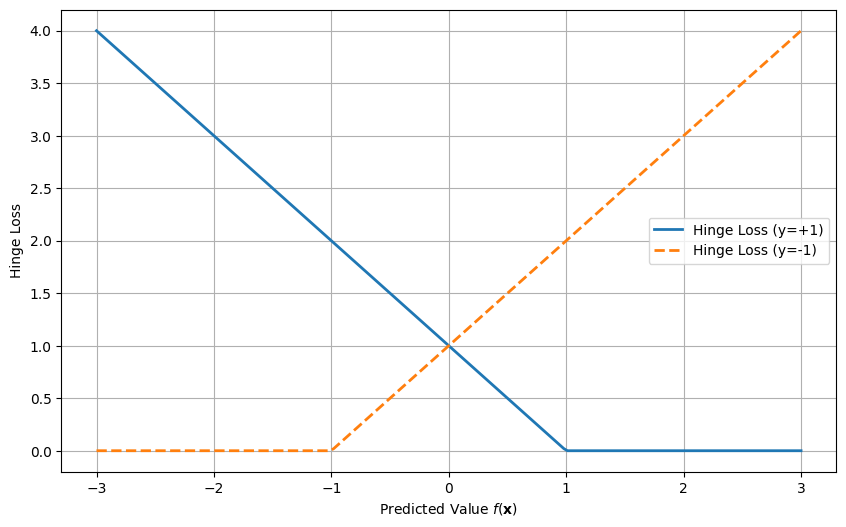
6.2.1. Hinge Loss (Used in Support Vector Machines)#

The hinge loss is commonly used in support vector machines (SVMs) and is defined as:

\[\mathcal{L}_{\text{hinge}} = \sum_i \max(0, 1 - y_i f(\mathbf{x}_i))\]

This loss penalizes any data points where the predicted value \(f(\mathbf{x}_i)\) does not match the true label \(y_i\). If \(y_i f(\mathbf{x}_i) \geq 1\), the prediction is correct and there is no penalty. If \(y_i f(\mathbf{x}_i) < 1\), there is a penalty proportional to the misclassification.

Hide code cell source 
import numpy as np
import matplotlib.pyplot as plt

# Define a wider range for f(x) to span from -3 to +3
f_x_wide = np.linspace(-3, 3, 200)

# Calculate hinge loss for y=1 and y=0 over the range of f(x) from -3 to +3
hinge_loss_y1 = np.maximum(0, 1 - f_x_wide)  # Hinge loss for y=1
hinge_loss_y0 = np.maximum(0, 1 + f_x_wide)  # Hinge loss for y=-1

# Plot the hinge loss for y=1 and y=0 over the wider range
plt.figure(figsize=(10, 6))
plt.plot(f_x_wide, hinge_loss_y1, label="Hinge Loss (y=1)", linestyle='-', linewidth=2)
plt.plot(f_x_wide, hinge_loss_y0, label="Hinge Loss (y=-1)", linestyle='--', linewidth=2)
plt.xlabel("Predicted Value $f(\\mathbf{x})$")
plt.ylabel("Hinge Loss")
plt.legend()
plt.grid(True)
plt.show()
../_images/a94576e5f12e881d8e4fe7258e48ce26f12971fdadaf143785133d2bd308b622.png

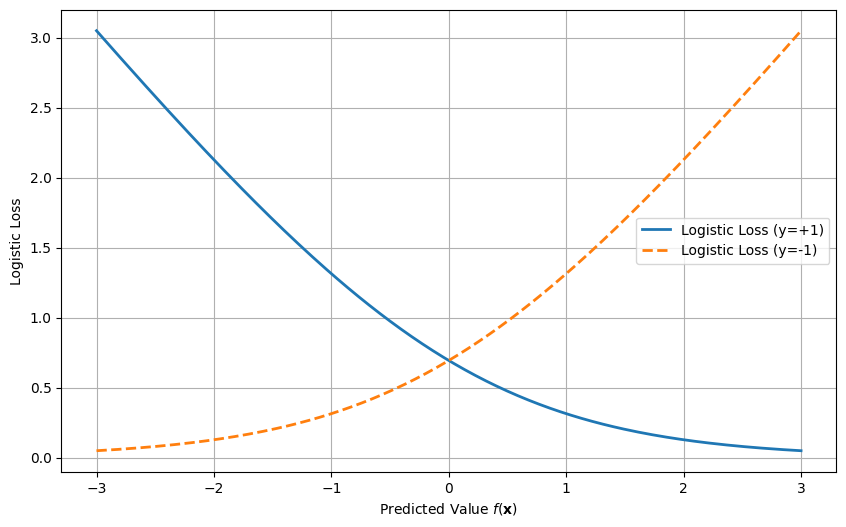
6.2.2. Logistic Loss (Used in Logistic Regression)#

The logistic loss is used in logistic regression and is defined as:

\[\mathcal{L}_{\text{logistic}} = \sum_i \log(1 + \exp(-y_i f(\mathbf{x}_i)))\]

This loss function provides a smooth gradient and penalizes incorrect predictions by increasing the loss for large errors. Logistic regression aims to minimize this loss while interpreting \(f(\mathbf{x}_i)\) as a probability.

Hide code cell source 
import numpy as np
import matplotlib.pyplot as plt

# Define a wider range for f(x) to span from -3 to +3
f_x_wide = np.linspace(-3, 3, 200)

# Recalculate logistic loss for the wider range of f(x) for y=1 and y=0
logistic_loss_y1_wide = np.log(1 + np.exp(-f_x_wide))  # Logistic loss for y=1
logistic_loss_y0_wide = np.log(1 + np.exp(f_x_wide))   # Logistic loss for y=-1

# Plot the logistic loss for y=1 and y=0 over the wider range
plt.figure(figsize=(10, 6))
plt.plot(f_x_wide, logistic_loss_y1_wide, label="Logistic Loss (y=1)", linestyle='-', linewidth=2)
plt.plot(f_x_wide, logistic_loss_y0_wide, label="Logistic Loss (y=-1)", linestyle='--', linewidth=2)
plt.xlabel("Predicted Value $f(\\mathbf{x})$")
plt.ylabel("Logistic Loss")
plt.legend()
plt.grid(True)
plt.show()
../_images/74ea8ccd2e6ca8f64d85056ec00ddbc3faa9093fc7ee951ad73f67a1ad015ca2.png

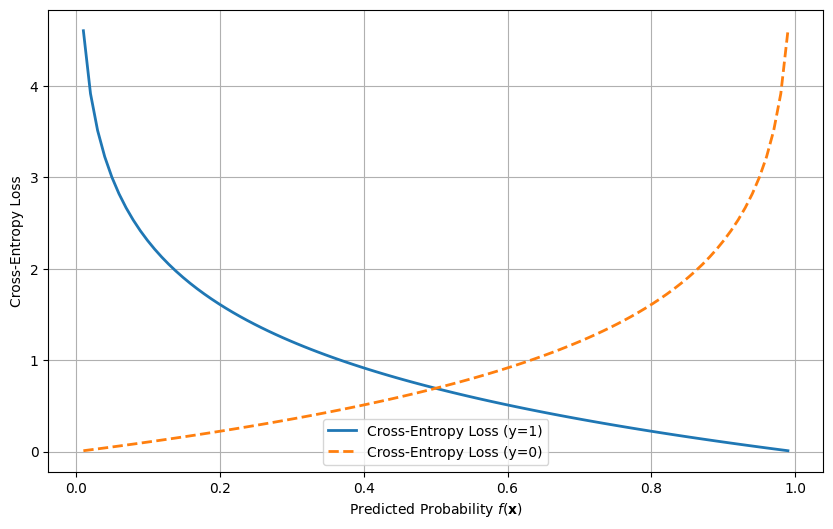
6.2.3. Cross-entropy loss#

The probably most used loss function for classification tasks is cross-entropy loss. This loss function measures the difference between the predicted probabilities and the actual class labels. It is defined as:

\[\mathcal{L}_{\text{cross-entropy}} = - \frac{1}{N} \sum_{i=1}^N \left( y_i \log(f(\mathbf{x}_i)) + (1 - y_i) \log(1 - f(\mathbf{x}_i)) \right)\]
Hide code cell source 
import numpy as np
import matplotlib.pyplot as plt

# Define the range of f(x) values from near zero to near one to avoid log(0)
f_x = np.linspace(0.01, 0.99, 100)

# Compute cross-entropy loss for y=1 and y=0
loss_y1 = -np.log(f_x)  # Cross-entropy loss when y=1
loss_y0 = -np.log(1 - f_x)  # Cross-entropy loss when y=0

# Plot the cross-entropy loss for y=1 and y=0
plt.figure(figsize=(10, 6))
plt.plot(f_x, loss_y1, label="Cross-Entropy Loss (y=1)", linestyle='-', linewidth=2)
plt.plot(f_x, loss_y0, label="Cross-Entropy Loss (y=0)", linestyle='--', linewidth=2)
plt.xlabel("Predicted Probability $f(\\mathbf{x})$")
plt.ylabel("Cross-Entropy Loss")
plt.legend()
plt.grid(True)
plt.show()
../_images/87c0aa732ae9d7a4ebd21d0ed9b054b68e9b9aaf7d1ce7b1320034ed9b4e3643.png

6.3. Classification Example: Logistic Regression#

Let’s look at a simple example where we use the concepts of regression to perform a classification task. In logistic regression, we aim to model the probability that a given data point belongs to class \(+1\) or class \(-1\).

The logistic function, also called the sigmoid function, is used to map the output of the linear function \(f(\mathbf{x})\) to a probability between 0 and 1:

\[P(y_i = +1 | \mathbf{x}_i) = \frac{1}{1 + \exp(-f(\mathbf{x}_i))}\]

Where \(f(\mathbf{x}_i) = \mathbf{x}_i^\top \beta\) is the linear function that we optimize. The logistic loss function is then minimized to find the best-fitting model.

6.4. Optimizing the Model for Classification#

To solve the classification task, we follow the same procedure used in regression:

  1. Define a loss function: For classification, this could be the hinge loss or logistic loss.

  2. Optimize the loss function: We minimize the loss function using methods like gradient descent or optimization tools.

  3. Make predictions: After fitting the model, we predict the class label based on the sign of \(f(\mathbf{x})\).

6.4.1. Example of Logistic Regression in Code#

import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from scipy.optimize import minimize

sns.set_style("whitegrid")

# Generate a simple dataset from two separate distributions
np.random.seed(0)

# Class +1 examples: centered at (0.5, 0.5)
X_pos = np.random.randn(50, 2) + 0.5
y_pos = np.ones(50)

# Class -1 examples: centered at (-0.5, -0.5)
X_neg = np.random.randn(50, 2) - 0.5
y_neg = -np.ones(50)

# Combine the datasets
X = np.vstack([X_pos, X_neg])
y = np.hstack([y_pos, y_neg])

# Sigmoid function
def sigmoid(z):
    return 1 / (1 + np.exp(-z))

# Logistic loss function
def logistic_loss(beta, X, y):
    z = X @ beta
    return np.sum(np.log(1 + np.exp(-y * z)))

# Initial guess for beta (weights)
initial_beta = np.zeros(X.shape[1])

# Minimize the logistic loss
result = minimize(logistic_loss, initial_beta, args=(X, y), method='BFGS')
optimized_beta = result.x

# Generate a grid of values for plotting the decision boundary
x1_range = np.linspace(X[:, 0].min() - 1, X[:, 0].max() + 1, 100)
x2_range = np.linspace(X[:, 1].min() - 1, X[:, 1].max() + 1, 100)
x1_grid, x2_grid = np.meshgrid(x1_range, x2_range)

# Compute the logistic regression decision boundary (p = 0.5)
z = optimized_beta[0] * x1_grid + optimized_beta[1] * x2_grid
probability = sigmoid(z)

# Create a plot with the data points and decision boundary
plt.figure(figsize=(8, 6))

# Plot the probability gradient
contour_plot = plt.contourf(x1_grid, x2_grid, probability, levels=50, cmap='coolwarm', alpha=0.7)

# Scatter plot of the dataset with class labels
sns.scatterplot(x=X[:, 0], y=X[:, 1], hue=y, palette="coolwarm", s=60, edgecolor='k')


# Add the decision boundary (p = 0.5)
# plt.contour(x1_grid, x2_grid, probability, levels=[0.5], colors='black', linestyles='--')

plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.grid(True)
# Add colorbar showing the predicted probability
plt.colorbar(contour_plot, label="Predicted Probability (Class +1)")

plt.show()
../_images/0c861853c1defaebf57181a4d076b09ef0861e5cb3668c3375949c668e1c02d9.png

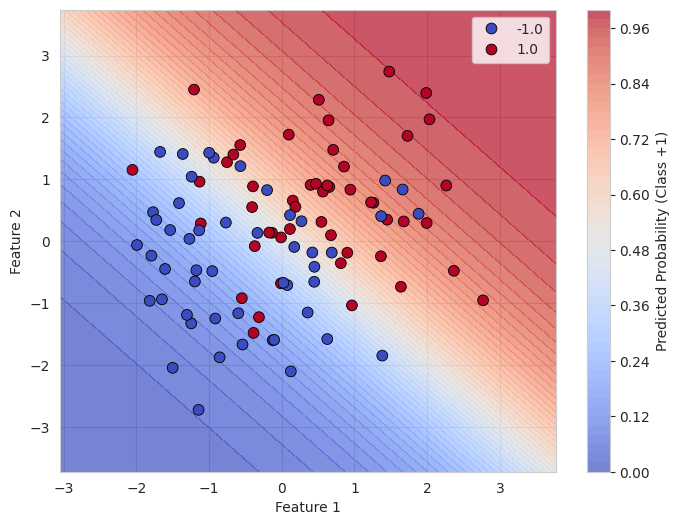
In this example:

  • Logistic Loss is minimized to fit a classification model.

  • The model predicts class labels \(y = \pm 1\), based on the sign of \(f(\mathbf{x})\).

  • The classification accuracy is calculated by comparing the predicted labels with the actual labels.

6.5. Summary#

By extending the concepts of regression to classification, we can use similar techniques, such as minimizing a loss function, to build classification models. By using specific loss functions like hinge loss or logistic loss, we adapt regression methods to classify data. This approach demonstrates how foundational ideas from regression can be applied to a wide range of machine learning tasks.

Contents